Describe the Translation in Each Function

G x 3 x 27. The parent function is the simplest form of the type of function given.

Using Transformations To Graph Functions

Notice that the function is of the form gx ax2 where a 1 2.

. у 3D x 51 3. Solution Lets break down h x first. The transformation from the first equation to the second one can be found by finding a a h h and k k for each equation.

Given the function fx x to gxx-5 if you look at the gx function you will see that 5 was subtracted from the abscissa x that is. Describe the translations applied on y x 3 to attain the function h x x 1 3 1. G x 5 8 x 25.

So the graph of g is a refl ection in the x-axis and a vertical shrink by a. Lets go ahead and graph x 3 first. The transformation being described is from gx x2 g x x 2 to f x x2 f x x.

W x x43 4 x4 Move 5 spaces left. Or is there some other verbatim that he needs to write. G x x 2 8 24.

Ok I can tell him how to graph most of these. The function v x x 3 4x. Then graph the function.

Up to 24 cash back translation of the graph of y x down 3 units Describe the reflection in each function. W x x53 4 x5 graph. Y x - 2 Does it just want him to say its a translation of the graph of x down 2 units.

This described the required translation. F x x2 f x x 2. Correct answer - Describe the translation in each function as it relates to the graph of fx x gx x 7 gx x-5 gx x2 gx x 75.

Y x2 4. Transformations of Quadratic Functions Describe the transformation of fx x2 represented by g. Y axhk y a x - h k.

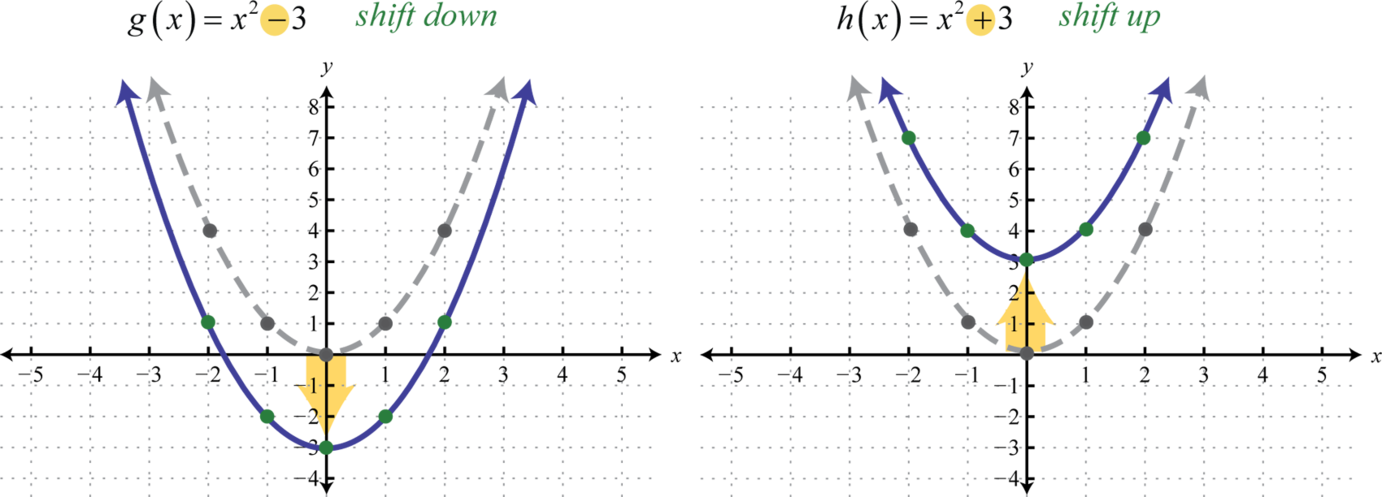
A column vector breaks down the translation into. For example the function y sin2x does not have period 2. Subtracting from the output of a function moves the graph down.

Move 3 spaces down. W x 2 x3 4x 2x3 8x. Step-by-step explanation Image transcriptions Question 1 y - x2 4x y - x2- 4x y - x-22 -4 y - x- 2 4 Parent y x 2 function Horizontal translation 2 unit right.

Just dont know what they. 628721 constant 628721 quadratic 628721 absolute value 628721 linear Describe the translation in each function. Identify the type of function represented by each graph.

To describe a translation we need to say in which direction and by what distance each point is moved. G x 25 x Transformations of Linear Functions Reveal Algebra 1. All answers are given below.

Gx fx - 5. Y x 2 5y x - 524 6. Gx 2x2 1 SOLUTION a.

G x 15 x Mixed Exercises Describe the transformation in each function as it relates to the graph of the parent function. Translations The graph of a function can be moved up down left or right by adding to or subtracting from the output or the input. But what is he supposed to describe.

G x x 4 23. A Identify the parent function f. Then graph the function.

G x 4 5 x 20. H is related to one of the six parent functions. Factor a 1 1 out of the absolute value to make the.

The original period divided by the constant b. The period is given by the fraction 2ˇ b ie. W x x3 4x 2.

628721 When a constant k is added to or subtracted from a parent function the result fx k is a translation of the graph up or down. Describe the Transformation f xx2. Gx x2 g x x 2.

Here are the graphs of y f x y f x 2 and y f x - 2. Move 4 spaces right. Hence we need to translate x 3 one unit to the right and one unit downward.

G x 1 5 x 26. Describe the translation of each trig function ysin 12xπ ycos 3x 2 y2sin x -34 Lets Answer The World. Move 2 spaces up.

165 reflection of the graph of y x2 across the x-axis 165 reflection of the graph of y x2 across the y-axis Describe the dilation in each function. Use the transformations to graph h x as well. Describe each translation as it relates to the graph of the parent function.

Vertical translation up 4 units. This shows that the function fx was translated to the left by 5 units to form gx. So for example the function y sin2x will have period 2ˇ 2 ˇbtells you the number of the cycles of the sine function on an interval of length 2ˇThus the graph of y sin2xconsists.

Y 5x 61-8 Use the graph of each translated parent function to write its equation. Y x-51-3 3y x-1 4. Here are some things we can do.

Then graph the function. Stretch it by 2 in the y-direction. How far a shape moves in the horizontal direction left or right.

We then apply the transformations. Solution for Describe the translation in each function as it relates to its parent graph. Describe the translation in each function as it relates to the graph of teh parent functiongxx-6gx-3xgxx- 112.

Reflection over x-axis. Y 5x 61-8 Use the graph of each translated parent function to write its equation. Then graph the function.

I dont know what theyre looking for there. Gx 1 STRUCTURE 2 x 2 b. H x 2 x 8 1.

F x x f x x gx x 5 g x x - 5. Y x2 4 2. Terms in this set 26 Fill in the y values of the t-table for the function y3 sqrt x -8 -2 -1 -1 00 1 1 8 2 Move the slider on the graph on the right to graph each function and describe the translation.

Function and position relative to parent left of the parent right of the parent below the parent above the parent. X - 524 6. B Describe the sequence of transformations from f to h.

H x x 1 3 1. C Sketch the graph of h by hand. Adding to the output of a function moves the graph up.

W x x3 4x 3. G x 6 x 21. 4 is added with x2.

Then graph each function. 15 January 2022 by lets tokmak. D Use function notation to write h in terms of the parent function f.

Using a Column Vector to Describe a Translation A column vector is used to describe a translation.

Horizontal Translation Concept Grapher Solved Examples Cuemath

How Do You Translate A Function Printable Summary Virtual Nerd

Horizontal Translation Concept Grapher Solved Examples Cuemath